6.5.2016

Měřením solárních článků jsem se zabýval ve svém předchozím zaměstnání. Protože teď se moje firma zabývá vývojem software na zakázku, nehodil jsem předchozí práci za hlavu a poskytuji podporu i pro starší aplikace. Měření solárních článků máme ostatně i mezi ukázkami naší práce.

Fill Factory

Výrobou a měřením solárních článků se v Rožnově zabývá firma Fill Factory. Program pro měření solárních článků zde funguje už dlouhé roky, drobné potíže se objevily až v poslední době, při měření nových ECN článků. Ty jsou ostatně natolik zajímavé, že jsem si dovolil jeden článek vyfotit:

Co se na článcích měří

Na solárních článcích se měří spousta různých parametrů - jedním z nejdůležitějších, které zajímají každého uživatele fotovoltaického článku, je výkon, který může článek dodávat.

V praxi se solární článek měří tak, že se připojí na zdroj napětí, které se postupně zvyšuje, a měří se proud protékající článkem. Vše probíhá při osvětlení odpovídajícímu plnému slunečnímu svitu. Výsledkem je několik stovek změřených párů hodnot napětí-proud, ze kterých lze dopočítat požadované parametry - mezi nimi i maximální výkon, který dokáže článek dodávat.

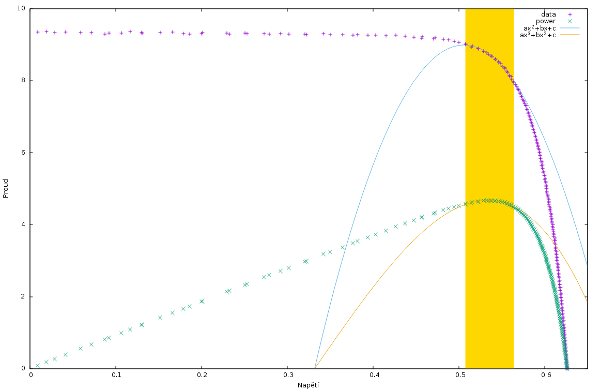
Na přiloženém obrázku jsou naměřené hodnoty nakreslené modrými znaky plus. Výkon dodávaný článkem se spočítá v každém bodě jednoduše:

    výkon = napětí × proud

Hodnoty výkonu jsou v grafu nakreslené zelenými křížky.

Pokud chceme najít maximální výkon, zdá se být úloha triviální: stačí spočítat výkon v každém naměřeném bodu a vybrat takový bod, ve kterém je hodnota výkonu nejvyšší.

Má to ale háček - rušení

I když na první pohled vypadá úloha jednoduše, v praxi naráží takový naivní přístup na nepřekonatelné potíže.

Řada naměřených hodnot totiž byvá často zarušená různými impulsy. Člověk i při letmém pohledu na graf rozezná, že některý bod je mimo a neměl by být do výpočtu zahrnutý - člověk dokáže takový bod odfiltrovat automaticky. Naivní algoritmus popsaný výše ale žádnou filtraci nemá a ochotně označí za bod maximálního výkonu jakoukoliv rušivou špičku, která se v datech náhodně objeví.

Data je tedy třeba nějakým způsobem filtrovat. Jako první mě napadlo použít nějaký digitální filtr. Naměřených hodnot ale není takové množství, aby mohl digitální filtr dobře fungovat. Užitečnější byl hned druhý nápad - použít pro hledání důležitých bodů na křivce regresní analýzu.

Použití regresní analýzy

Bodů, které se na křivce hledají, je více. Křivka na grafu není kompletní - naměřené hodnoty pokračují i mimo graf. Důležitými parametry jsou například hodnoty napětí a proudu v místech, kde křivka protíná osy x a y, stejně tak i sklon křivky v těchto bodech. Zde je možné použít regresní analýzu velmi jednoduše, protože v okolí obou bodů lze křivku snadno nahradit přímkou.

Celá křivka je modelovaná exponenciální rovnicí

    y = a + becx

S takovou rovnicí se mi ale velmi špatně pracuje. Pro hledání minimální chyby v regresní analýze je potřeba rovnici zderivovat, na což moje matematické kungfu nestačí. Napadlo mě ale nahradit zajímavou část křivky polynomem. Prakticky stačí pro blízké okolí bodu maximálního výkonu použít parabolu:

    y = ax² + bx + c

Potřebné vztahy pro regresi paraboly je pak snadné opsat do programu z učebnice statistiky.

V obrázku je rozmezí hodnot, ve kterém se křivka nahrazuje polynomem (zde parabolou), vyznačená žlutým pruhem, parabola samotná je pak nakreslená modrou barvou.

Nalezení bodu maximálního výkonu

Pokud je charakteristika článku vyjádřena jako

    y = ax² + bx + c

potom výkon je

    P = ax³ + bx² + cx

V obrázku je namodelovaná křivka výkonu nakreslená oranžovou barvou, vyznačený žlutý pruh pak ukazuje, které hodnoty byly pro vypočtení křivky použité.

Při hledání maximálního výkonu se hledá bod, ve kterém je derivace výkonu nulová:

    (ax³ + bx² + cx)' = 3ax² + 2bx + c = 0

Celý problém se pak zredukuje na vyřešení kvadratické rovnice.

Zdroj potíží

Při měření solárních článků se objevily problémy se špatným určením maximálního výkonu. Problém byl v příliš širokém rozmezí bodů, které vstupovaly do hledání modelové křivky. Nové, větší články, které ve Fill Factory vyrábějí, mají ostřejší koleno křivky a nalezená parabola modelující křivku se nadokázala zakroutit dostatečně rychle. Zdroj potíží velice rychle odhadnul Aleš Poruba. Při podrobném zkoumání naměřených hodnot se jeho odhad bezpečně potvrdil.